I had the pleasure of doing an interview of sorts with Leo Lopez, MD, the lead author and PI of the recent Pediatric Heart Network z-score manuscript. There are probably bigger and more insightful questions to ask, but these are the ones I posed.
A big "Thank You" to Leo and the PHN group for indulging me this opportunity.
Q.
Just a small matter of methods and results: We know the age range (0-18 years) and that obesity was an excluding criterion, but what were the height and weight ranges? That is, to which of our patients do these data apply?
A.
Height range: 43.2 - 207.2 cm (mean 117.1 ± 44.8 cm, median 120 cm);
weight range 2.0 - 122.6 kg (mean 30.2 ± 23.5 kg, median 22.6 kg).
Q.
So why are there no data for end systolic dimension/length/area/volume - or function?
A.
There are likely other confounding factors other than body size and/or age that affect LV end-systolic size parameters as well as LV systolic functional parameters - we did not explore these factors in our study. In addition, the reported variability for these parameters are different than the variability reported for the other parameters presented in the paper. Consequently, we decided to study these parameters more carefully in terms of predictors and variability and will publish our findings when these analyses are complete.
Q.
Given the limitations of BSA as a scaling variable, what was the discussion like concerning using lean body mass (estimated or otherwise), or a multivariable model using height and weight independently (Dallaire et al) for normalizing body size?
A.
We knew there were limitations with using BSA as a predictor of cardiovascular size in the obese population, particularly when normalizing LV mass. However, BSA still remains as the best predictor of LV mass in the normal population. Thus, our study evaluating a normal population specifically excluded obese subjects because of the associated cardiovascular pathology reported with obesity. With exclusion of the obese population, BSA was appropriate for allometric scaling in our normal study population. We did not consider an analysis using estimated lean body mass as a predictor of cardiovascular sizes given the variability of and limitations with the formulas used to estimate lean body mass. In addition, measuring lean body mass using DEXA technology was outside of the scope of this study because of its retrospective design and the use of DEXA is not standard practice when obtaining an echocardiogram. As for multivariable models using height and weight independently as well as other models using other transformations of BSA, we decided to focus primarily on the physiologic approach described by Sluysmans and Colan to normalize the sizes of cardiovascular structures for body size. As discussed in the paper, many models utilize a rigorous statistical approach to find the "best fit" for each parameter (with logarithmic or polynomial regressions), but most do not have physiologic justification for the statistical approach. In addition, these types of models result in very complex methods to calculate Z-scores, often requiring the use of the LMS method to account for age-dependent variations in the regression equations. The analyses of the PHN study resulted in a model that utilized a single and simple methodology to predict the sizes of cardiovascular structures with BSA, so additional models using other body size parameters were not evaluated. Having said that, we are now considering a similar study to evaluate height as the scaling variable for the overweight population (BMI 85th - 95th percentile) and weight for children less than 2 years of age.
Q.
The data are described as being "normally distributed"— a requirement in order that they be used as z-scores. How were the distributions tested or confirmed?
A.
A histogram was constructed for each indexed parameter, and the normality of the distribution was subjectively or qualitatively determined. We did not do formal statistical testing because most methods to test for normality are quite sensitive to even small departures from normality. This would be problematic given our large sample size.
Q.
The new data depart somewhat from previous z-score models wherein the mean and SD are modeled, and z-scores are based on those models. The approach for the new data is to determine and calculate an appropriate allometric indexed value, and the z-scores are then [derived] for indexed values. What was the inspiration for this decision? Was there consensus among the group that this was a good idea?
A.
We actually tried multiple approaches to describe the relationship between parameter size and BSA after we finished collecting our data. Because we knew that our large sample size would allow us to evaluate the effects of race and ethnicity on this relationship, we wanted to use a model that would incorporate race and ethnicity (as well as BSA, age, and sex) into the Z-scores. This necessitated modeling the relationship between the parameters and BSA when a linear relationship was clearly not the appropriate assumption. The allometric indexed parameters turned out to model this relationship well, thereby simplifying the Z-score approach. This was very much a group effort, with consensus reached for each step along the way.
Q.
This particular form of ratiometric correction has been derided in the past, owing to its often inappropriate application, i.e., not meeting defining criteria. The conditions the data for a ratiometric correction must meet are these:
- linear relationship between the variables
- zero intercept
- homoscedasticity
What evidence is presented to the readers such that we may know the new data meet the requirements for a proper ratiometric correction?
A.
- We tested for any residual relationship between the indexed parameters and BSA using clinical significance rather than statistical significance, given our large sample size. Thus, we chose the appropriate exponent to transform BSA for each parameter only if there was a nearly zero slope (within the limits of clinical significance) when plotting the indexed parameter against BSA. This, in turn, assured a linear relationship between the indexed parameter and the transformed BSA.
- The relationship that we tested for each parameter was of the form y = mxa and not y = mxa +b (m = some constant), wherein the former assumes a zero intercept whereas the latter an intercept of b. We were able to determine models that used the 1st equation with the zero intercept for all parameters. In addition, we plotted all of the raw parameter values against the transformed BSA for that parameter, and in all instances the regression line would have had an approximately zero intercept (since there were no subjects with a zero BSA, this was extrapolated from the graphs).
- We observed increased variance for most parameters with increasing BSA values, but this was not observed for the indexed parameters (all of which were normally distributed) once we chose the appropriate BSA transformation exponent.
Q.
According to the manuscript, for most relationships the slope of the indexed value vs. BSA was significantly different from zero, indicating some residual dependence on BSA. As a test to see if this slope was clinically important, values from the 1st and 3rd quartiles of BSA were compared between the actual model and a true zero slope. Those differences were evaluated and found to be equal to or less than 5%, and thus, deemed clinically unimportant. It occurs to me that the slope of a line could be within a particular margin at one point, but at points further out the divergence could become clinically significant. Considering that an appropriate index should be valid over the entire range of body size, what is the rationale behind using the quartiles as checkpoints? Should we be worried?
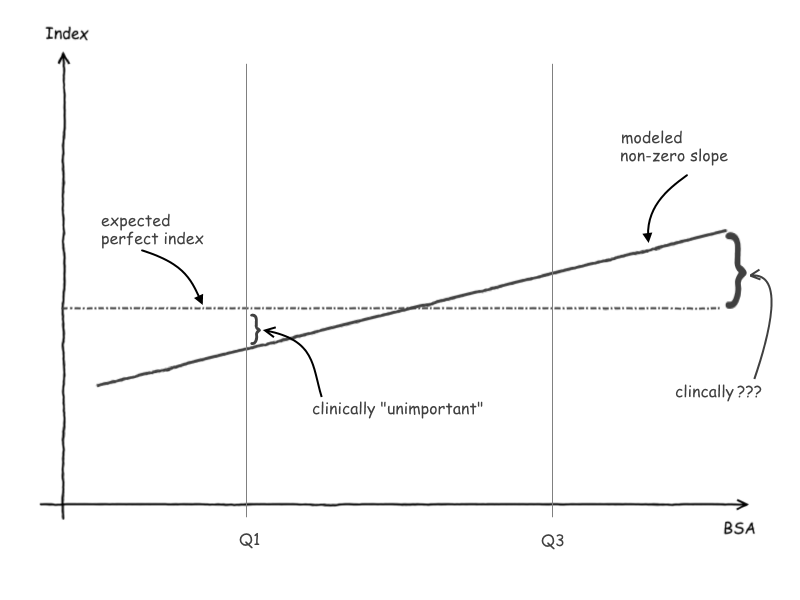
A.
This is very good point. There was definitely the possibility that our conclusions would not be valid on either side of the 1st and 3rd BSA quartile. Consequently, we ran a similar analysis looking at the percent difference of raw parameter values at the 5th and 95th percentile of BSA for all of the parameters in the study. In this analysis, the percent difference was greater than 5% for only 4 of the parameters (it was 7% or less for all the parameters).
Q.
Lastly, the PHN website notes that ECG data was also collected during this trial for future establishment of ECG reference values. How is that coming and can we look forward to eventually doing fewer echo studies for the indication possible LVH?
A.
The PHN paper listing new pediatric ECG reference values is currently under review. The Normal ECG Project is now testing whether age, sex, and/or race have a significant effect in addition to BSA on these reference values.
